MiniDES
实验内容
能够对任意64bit明文和64bit密钥,加密得到64bit密文,并在相同密钥下解密还原出明文。 不能有加密后不能解密的现象,不能有明显等效的不相同密钥。 对于随机明文和密钥,统计输入变化任1bit,输出密文变化bit数(应在0~64之间)。输出1000000统计结果(结果应该在32bit附近形成正态分布) 在满足以上要求的前提下,测速。速度越快越好。
DES
数据加密标准(英语:Data Encryption Standard,缩写为 DES)是一种对称密钥加密块密码算法,1976年被美国联邦政府的国家标准局确定为联邦资料处理标准(FIPS),随后在国际上广泛流传开来。它基于使用56位密钥的对称算法。这个算法因为包含一些机密设计元素,相对短的密钥长度以及怀疑内含美国国家安全局(NSA)的后门而在开始时有争议,DES因此受到了强烈的学院派式的审查,并以此推动了现代的块密码及其密码分析的发展。
DES现在已经不是一种安全的加密方法,主要因为它使用的56位密钥过短。1999年1月,distributed.net与电子前哨基金会合作,在22小时15分钟内即公开破解了一个DES密钥。也有一些分析报告提出了该算法的理论上的弱点,虽然在实际中难以应用。为了提供实用所需的安全性,可以使用DES的派生算法3DES来进行加密,虽然3DES也存在理论上的攻击方法。DES标准和3DES标准已逐渐被高级加密标准(AES)所取代。另外,DES已经不再作为国家标准科技协会(前国家标准局)的一个标准。
算法描述
DES是一种典型的块密码—一种将固定长度的明文通过一系列复杂的操作变成同样长度的密文的算法。对DES而言,块长度为64位。同时,DES使用密钥来自定义变换过程,因此算法认为只有持有加密所用的密钥的用户才能解密密文。密钥表面上是64位的,然而只有其中的56位被实际用于算法,其余8位可以被用于奇偶校验,并在算法中被丢弃。因此,DES的有效密钥长度仅为56位。
整体结构
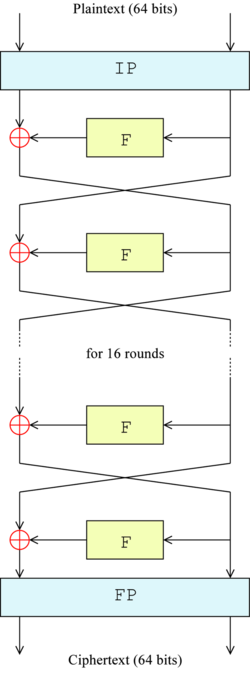
算法的整体结构如图所示:有16个相同的处理过程,称为“回次”(round),并在首尾各有一次置换,称为IP与FP(或称IP-1,FP为IP的反函数(即IP“撤销”FP的操作,反之亦然)。IP和FP几乎没有密码学上的重要性,为了在1970年代中期的硬件上简化输入输出数据库的过程而被显式的包括在标准中。
在主处理回次前,数据块被分成两个32位的半块,并被分别处理;这种交叉的方式被称为费斯妥结构。费斯妥结构保证了加密和解密过程足够相似—唯一的区别在于子密钥在解密时是以反向的顺序应用的,而剩余部分均相同。这样的设计大大简化了算法的实现,尤其是硬件实现,因为没有区分加密和解密算法的需要。
图中的⊕符号代表异或(XOR)操作。“F函数”将数据半块与某个子密钥进行处理。然后,一个F函数的输出与另一个半块异或之后,再与原本的半块组合并交换顺序,进入下一个回次的处理。在最后一个回次完成时,两个半块需要交换顺序,这是费斯妥结构的一个特点,以保证加解密的过程相似。
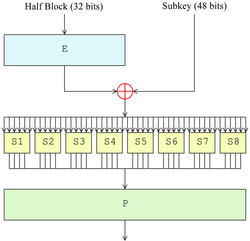
费斯妥函数(F函数)
图中显示了费斯妥函数(F函数)的过程。其每次对半块(32位)进行操作,并包括四个步骤:
-
扩张—用扩张置换(图中的E)将32位的半块扩展到48位,其输出包括8个6位的块,每块包含4位对应的输入位,加上两个邻接的块中紧邻的位。
-
与密钥混合—用异或操作将扩张的结果和一个子密钥进行混合。16个48位的子密钥—每个用于一个回次的F变换—是利用密钥调度从主密钥生成的(见下文)。
-
S盒—在与子密钥混合之后,块被分成8个6位的块,然后使用“S盒”,或称“置换盒”进行处理。8个S盒的每一个都使用以查找表方式提供的非线性的变换将它的6个输入位变成4个输出位。S盒提供了DES的核心安全性—如果没有S盒,密码会是线性的,很容易破解。
-
置换—最后,S盒的32个输出位利用固定的置换,“P置换”进行重组。这个设计是为了将每个S盒的4位输出在下一回次的扩张后,使用4个不同的S盒进行处理。 S盒,P置换和E扩张各自满足了克劳德·香农在1940年代提出的实用密码所需的必要条件,“混淆与扩散”。
密钥生成
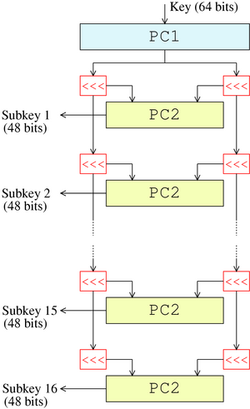
首先,使用选择置换1(PC-1)从64位输入密钥中选出56位的密钥—剩下的8位要么直接丢弃,要么作为奇偶校验位。然后,56位分成两个28位的半密钥;每个半密钥接下来都被分别处理。在接下来的回次中,两个半密钥都被左移1或2位(由回次数决定),然后通过选择置换2(PC-2)产生48位的子密钥—每个半密钥24位。移位(图中由«标示)表明每个子密钥中使用了不同的位,每个位大致在16个子密钥中的14个出现。
解密过程中,除了子密钥输出的顺序相反外,密钥调度的过程与加密完全相同。
安全分析
暴力破解
对于一切密码而言,最基本的攻击方法是暴力破解法—依次尝试所有可能的密钥。密钥长度决定了可能的密钥数量,因此也决定了这种方法的可行性。对于DES,即使在它成为标准之前就有一些关于其密钥长度的适当性的问题,而且也正是它的密钥长度,而不是理论密码分析迫使它被后续算法所替代。在设计时,在与包括NSA在内的外部顾问讨论后,密钥长度被从128位减少到了56位以适应在单芯片上实现算法。
在学术上,曾有数个DES破解机被提出。1977年,迪菲和海尔曼提出了一部造价约2千万美元的破解机,可以在一天内找到一个DES密钥。1993年,迈克尔·维纳设计了一部造价约1百万美元的破解机,大约可以在7小时内找到一个密钥。然而,这些早期的设计并没有被实现,至少没有公开的实现。在1990年代晚期,DES开始受到实用的攻击。1997年,RSA安全赞助了一系列的竞赛,奖励第一个成功破解以DES加密的信息的队伍1万美元,洛克·韦尔谢什(Rocke Verser),马特·柯廷(Matt Curtin)和贾斯廷·多尔斯基(Justin Dolske)领导的DESCHALL计划获胜,该计划使用了数千台连接到互联网的计算机的闲置计算能力。1998年,电子前哨基金会(EFF,一个信息人权组织)制造了一台DES破解机,造价约$250,000。该破解机可以用稍多于2天的时间暴力破解一个密钥,它显示了迅速破解DES的可能性。EFF的动力来自于向大众显示DES不仅在理论上,也在实用上是可破解的。
一个确认的DES破解机是2006年由德国的鲁尔大学与基尔大学的工作组建造的COPACOBANA。与EFF的不同,COPACOBANA由商业上可获得的,可重配置的FPGA组成。120片并行的XILINX Spartan3-1000型FPGA分为20个DIMM模块,每个模块包括6个FPGA。使用可重配置的FPGA使得这种设备也可以用于其它密码的破解。另外一个关于COPACOBANA的有趣事实是它的成本。一台COPACOBANA的造价大约是$10,000,是EFF设备的25分之一,这充分说明了数字电路的持续进步。考虑到通货膨胀因素,同样价格的设备的性能在8年间大约提到了30倍。2007年,COPACOBANA的两个项目参与者组建的SciEngines公司改进了COPACOBANA,并发展了它的下一代。2008年,他们的COPACOBANA RIVYERA将破解DES的时间减少到了1天以内,使用128片Spartan-3 5000型FPGA。目前SciEngines的RIVYEAR保持着使用暴力破解法破解DES的纪录。
其他攻击方法
有三种已知方法可以以小于暴力破解的复杂性破解DES的全部16回次:差分密码分析(DC),线性密码分析(LC),以及戴维斯攻击。然而,这些攻击都是理论性的,难以用于实践;它们有时被归结于认证的弱点。
- 差分密码分析在1980年代晚期由艾力·毕汉姆和阿迪·萨莫尔重新发现;1970年代IBM和NSA便发现了这种方法,但没有公开。为了破解全部16回次,差分密码分析需要247组选择明文。DES被设计为对DC具有抵抗性。
- 线性密码分析由松井充(Mitsuru Matsui)发现,需要243组已知明文[38];该方法已被实现,是第一种公开的实验性的针对DES的密码分析。没有证据显示DES的设计可以抵抗这种攻击方法。一般概念上的LC—“多线性密码分析”—在1994年由Kaliski和Robshaw所建议,并由比留科夫等人于2004年所改进。线性密码分析的选择明文变种是一种类似的减少数据复杂性的方法。帕斯卡尔·朱诺德(Pascal Junod)在2001年进行了一些确定线性密码分析的实际时间复杂性的实验,结果显示它比预期的要快,需要约239–241次操作。
- 改进的戴维斯攻击:线性和差分密码分析是针对很多算法的通用技术,而戴维斯攻击是一种针对DES的特别技术,在1980年代由唐纳德·戴维斯(Donald Davies)首先提出,并于1997年为毕汉姆和亚历克斯·比留科夫(Alex Biryukov)所改进。其最有效的攻击形式需要250已知明文,计算复杂性亦为250,成功率为51%。 也有一些其它的针对削减了回次的密码版本,即少于16回次的DES版本。这些攻击显示了多少回次是安全所需的,以及完整版本拥有多少“安全余量”。差分线性密码分析于1994年为兰福德(Langford)和海尔曼所提出,是一种组合了差分和线性密码分析的方法。一种增强的差分线性密码分析版本可以利用$2^{15.8}$组已知明文可以以$2^{29.2}$的时间复杂性破解9回次的DES。
次要密码学特性
DES有补码特性,即
$E_K(P)=C\Leftrightarrow E_{\bar{K}}(\bar{P})=\bar{C}$,这样的性质表明暴力破解的工作量在选择明文攻击下可以减少一半。
DES有四个所谓的弱密钥。若使用弱密钥,加密和解密有相同的效果:
$E_K(E_K(P))=P$ 或 $E_K=D_K$
也有6对半弱密钥。若使用某个半弱密钥 $K_1$ 进行加密,则相当于使用其对应的半弱密钥 $K_2$ 进行解密:
$E_{K_1}(E_{K_2}(P))=P$ 或 $E_{K_2}=D_{K_1}$
在实现中可以轻易的避开弱密钥和半弱密钥,可以显式的测试密钥,或简单的随机选择密钥:刚好选到弱或半弱密钥的可能性几乎没有。这些密钥事实上并不比其它的密钥弱,因为他们没有给攻击以任何可利用的好处。
DES也被证明不是群,或更精确的,集合 ${E_k}$(对于所有可能的密钥 $K$)在复合函数之下不是一个群,也不“近似”于一个群。这有时是一个开放式的问题,而且若是这种情况,破解DES是可能的,且类似于3DES的加密模式不能增加其安全性。
DES的最大密码学安全性被限制在了约64位,除非独立选择每个回次的子密钥而不是从密钥中生成,这样做可以将允许768位的安全性。
算法实现
密钥生成
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
// pt is plain text
string pt, key;
/*cout<<"Enter plain text(in hexadecimal): ";
cin>>pt;
cout<<"Enter key(in hexadecimal): ";
cin>>key;*/
pt = "123456ABCD132536";
key = "AABB09182736CCDD";
// Key Generation
// Hex to binary
key = hex2bin(key);
// Parity bit drop table
int keyp[56] = { 57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4 };
// getting 56 bit key from 64 bit using the parity bits
key = permute(key, keyp, 56); // key without parity
// Number of bit shifts
int shift_table[16] = { 1, 1, 2, 2,
2, 2, 2, 2,
1, 2, 2, 2,
2, 2, 2, 1 };
// Key- Compression Table
int key_comp[48] = { 14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32 };
// Splitting
string left = key.substr(0, 28);
string right = key.substr(28, 28);
vector<string> rkb; // rkb for RoundKeys in binary
vector<string> rk; // rk for RoundKeys in hexadecimal
for (int i = 0; i < 16; i++) {
// Shifting
left = shift_left(left, shift_table[i]);
right = shift_left(right, shift_table[i]);
// Combining
string combine = left + right;
// Key Compression
string RoundKey = permute(combine, key_comp, 48);
rkb.push_back(RoundKey);
rk.push_back(bin2hex(RoundKey));
}
加解密
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// Hexadecimal to binary
pt = hex2bin(pt);
// Initial Permutation Table
int initial_perm[64] = { 58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7 };
// Initial Permutation
pt = permute(pt, initial_perm, 64);
cout << "After initial permutation: " << bin2hex(pt) << endl;
分为两部分
1
2
3
4
5
// Splitting
string left = pt.substr(0, 32);
string right = pt.substr(32, 32);
cout << "After splitting: L0=" << bin2hex(left)
<< " R0=" << bin2hex(right) << endl;
扩展表,以及 S 盒,以及置换表:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
// Expansion D-box Table
int exp_d[48] = { 32, 1, 2, 3, 4, 5, 4, 5,
6, 7, 8, 9, 8, 9, 10, 11,
12, 13, 12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21, 20, 21,
22, 23, 24, 25, 24, 25, 26, 27,
28, 29, 28, 29, 30, 31, 32, 1 };
// S-box Table
int s[8][4][16] = { { 14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13 },
{ 15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9 },
{ 10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12 },
{ 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14 },
{ 2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3 },
{ 12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13 },
{ 4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12 },
{ 13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11 } };
// Straight Permutation Table
int per[32] = { 16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25 };
Feistel 结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
for (int i = 0; i < 16; i++) {
// Expansion D-box
string right_expanded = permute(right, exp_d, 48);
// XOR RoundKey[i] and right_expanded
string x = xor_(rkb[i], right_expanded);
// S-boxes
string op = "";
for (int i = 0; i < 8; i++) {
int row = 2 * int(x[i * 6] - '0') + int(x[i * 6 + 5] - '0');
int col = 8 * int(x[i * 6 + 1] - '0') + 4 * int(x[i * 6 + 2] - '0') + 2 * int(x[i * 6 + 3] - '0') + int(x[i * 6 + 4] - '0');
int val = s[i][row][col];
op += char(val / 8 + '0');
val = val % 8;
op += char(val / 4 + '0');
val = val % 4;
op += char(val / 2 + '0');
val = val % 2;
op += char(val + '0');
}
// Straight D-box
op = permute(op, per, 32);
// XOR left and op
x = xor_(op, left);
left = x;
// Swapper
if (i != 15) {
swap(left, right);
}
cout << "Round " << i + 1 << " " << bin2hex(left) << " "
<< bin2hex(right) << " " << rk[i] << endl;
}
最后将左部和右部结合并置换:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// Combination
string combine = left + right;
// Final Permutation Table
int final_perm[64] = { 40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25 };
// Final Permutation
string cipher = bin2hex(permute(combine, final_perm, 64));
return cipher;
加密函数:
1
2
3
cout << "\nEncryption:\n\n";
string cipher = encrypt(pt, rkb, rk);
cout << "\nCipher Text: " << cipher << endl;
解密函数:
1
2
3
4
5
cout << "\nDecryption\n\n";
reverse(rkb.begin(), rkb.end());
reverse(rk.begin(), rk.end());
string text = encrypt(cipher, rkb, rk);
cout << "\nPlain Text: " << text << endl;
运行结果:
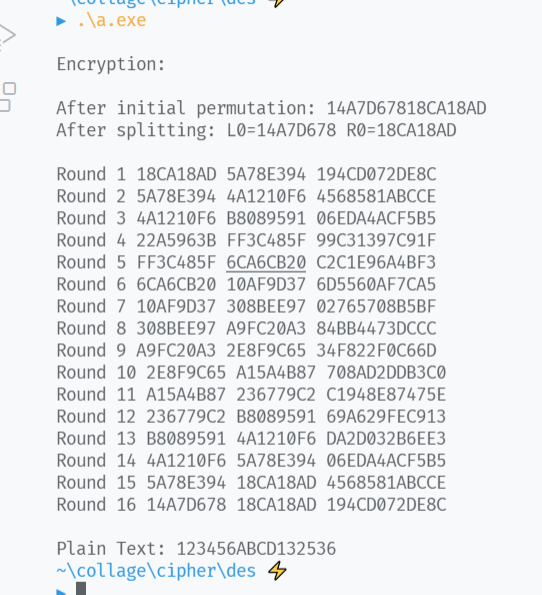
速度测试
为了方便编码、扩展位数、弄清楚DES的原理,使用了string作为密码算法的输入,所以算法的速度应该会比较慢一些。加解密流程是一致的,下面仅测试加密速度:
1
2
3
4
5
6
7
clock_t s = clock();
string cipher = encrypt(pt, rkb, rk);
clock_t e = clock();
double duration = (double)(e - s) / CLOCKS_PER_SEC;
cout << "time : " << duration * 1000
<< "ms, " << "speed : " << 64 / duration << " bit/s";
cout << "\nCipher Text: " << cipher << endl;
运行结果:
扩散混淆分析
统计不同的比特个数,以及随机改变比特:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int bit_diffrence(string a, string b) {
int diff = 0;
if (a.size() != b.size()) return -1;
for (int i = 0; i < a.size(); i++) {
if (a[i] == b[i]) diff++;
}
return diff;
}
string random_change_bit(string s) {
string ans = s;
int rnd = rand() % ans.size();
if (s[rnd] == '0') ans[rnd] = '1';
else ans[rnd] = '0';
return ans;
}
运行1000000次,并运行并统计:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int max_cnt = 1000000;
int bits_cnt[64] = {0};
string pt_bin = hex2bin(pt);
string cipher = encrypt_bin(pt_bin, rkb, rk);
for (int i = 0; i < max_cnt; i++) {
if (i % 100 == 0)
cout << double(i) / 1000 << "%" << endl;
string tmp = random_change_bit(pt_bin);
string cipher_tmp = encrypt_bin(tmp, rkb, rk);
int diff = bit_diffrence(cipher, cipher_tmp);
bits_cnt[diff - 1]++;
}
for (int i = 0; i < 64; i++) {
printf(", %d" + (!i) * 2, bits_cnt[i]);
}
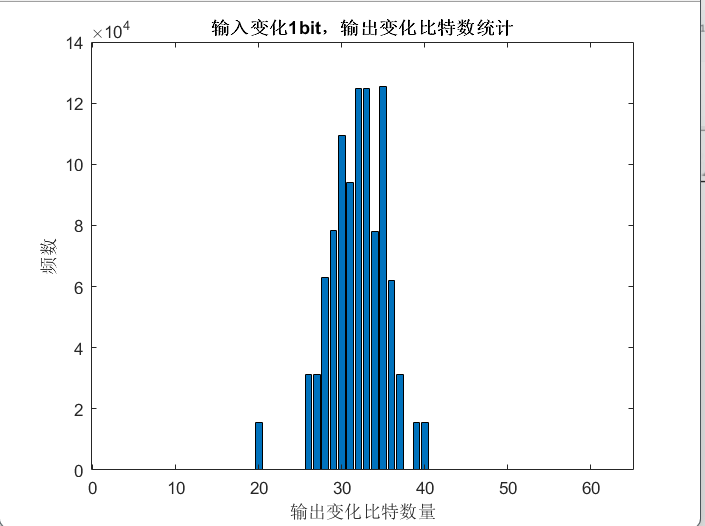
结果:

可视化结果,可见大致呈现正态分布,均值在32左右:
参考资料
资料加密标准 - 维基百科,自由的百科全书 (wikipedia.org)